If one have function and its inverse testing that latter is really inverse seems to be straightforward. All we need is to generate bunch of random values, apply function in question then its inverse and check that result is same as original value. It’s exactly what QuickCheck does.

However things become much more complicated when calculation with floating point are involved. Even if both function are correct result of consecutive function application could be very far off from expected value. By correct I mean that approximation agrees with exact value in N digits. But it’s to be expected. Calculations with floating point are full of such surprises. More interesting question is when precision loss occurs.

Let denote by \(f\) and \(f^{-1}\) exact functions which we approximate using floating point arithmetics. What we really calculate is following quantity where \(\varepsilon\) and \(\varepsilon'\) are rounding errors introduced by \(f\) and \(f^{-1}\) correspondingly:

\[ x' = f^{-1}\left[\, f(x)(1+\varepsilon) \right](1 + \varepsilon') \]

On next step we Taylor expand this expression and drop terms quadratic in \(\varepsilon\) (They are small!):

\[ x' \approx x \left(1 + \frac{f(x)}{f'(x)}\varepsilon + \varepsilon' \right)\]

This means rounding error introduced by \(f\) have enhacement or supression factor equal to \(f(x)/f'(x)\). Plot below visualize error propagation:

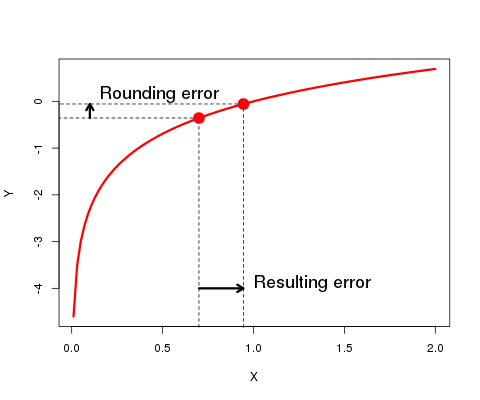
It’s easy to see that when derivartive of \(f(x)\) is small rounding error are greatly enhanced. There is other way to look at this. Function with small derivative squeezes many initial states into much smaller number of possible outputs so we lose information and consequently precision. This information loss is artifact of discretization. No information is lost in \(\mathbb{R} \to \mathbb{R}\) functions.

Second possibility is when \(f(x)\) is large. It’s best illustrated with following example:

\[ f(x) = x + a \qquad f^{-1}(x) = x - a \]

When \(|a| \gg |x|\) last digis of \(x\) are lost during addition and subtraction will not recover them.

Next plot visualize error in for functions \(f(x) = \arctan(x)\) and \(f^{-1} = \tan(x)\) together with error estimates which use formula above. Since we don’t know exact rounding error for every function evaluation machine epsilon is substituted for both \(\varepsilon\) which gives upper bound on error.

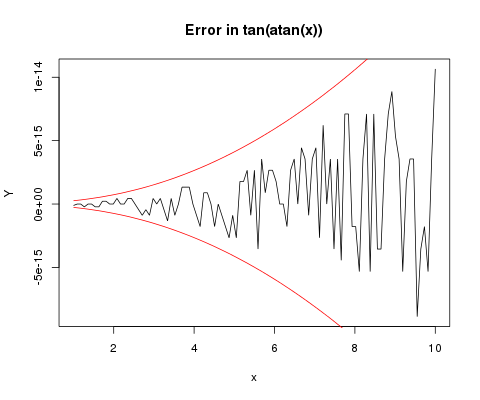
For reasont I don’t fully understand it overestimate error but gives reasonable overall agreement.

Links

• Home page
• All posts
• RSS feed

Tags