Criterion is excellent benchmarking framework. It easily could be the best one. It’s easy to use, able to generate nice reports. It attempts to get estimate of benchmark run time and error of this estimate. Strangely I never saw attempts to validate these measurements. Criterion is widely used but many questions important questions are still open:

1. Are measurements biased? OS scheduler and GC pauses tend to increase benchmark running time make distribution of run times asymmetric with tail at large t. This could easily lead to biased results.

2. Are error estimates reliable? Criterion could under- or overestimate errors. They are overlooked most of the time but still worth checking.

3. How precise are measurements. It’s easy to see 200% difference and be sure that it exists. But what about 20%? Or even 5%? What is measurable difference?

4. And of course there’s something else. There’s always something unexpected.

Correctness of error estimates

In this post I’ll try to check whether error estimates are reliable. This is very simple test. Measure same quantity many times and check what part of measurement fall into confidence interval. If too small fraction of event falls in error are underestimated and overestimated otherwise. All measurements were done with GHC 7.6.1 and criterion-0.6.2.1.

Here is program I used. It benchmarks exp function 1000 times. exp is cheap so here we probing regime of cheap functions which take many iterations to measure.

import Criterion.Main

main :: IO ()
main = defaultMain $ replicate 1000 $ bench "exp" $ nf exp (1 :: Double)

Benchmark was run on 6-core AMD Phenom-II with active X session. First thing to plot it run time vs number of benchmark. Here it is:

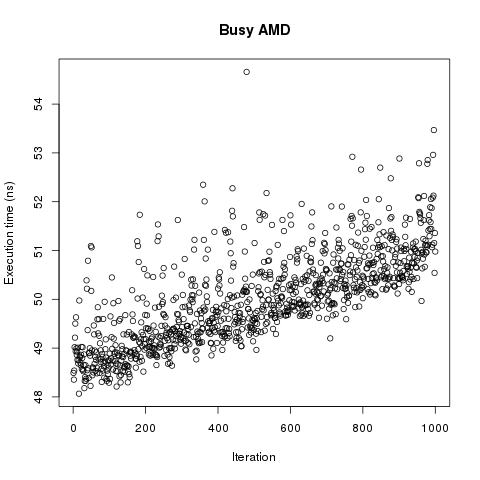
Now we have problem. Run time linearly depends on the number of benchmark or on the time. This test doesn’t discriminate between them. There is little doubt in existence of the effect but let repeat measurements in cleaner conditions. Second run was performed on completely idle core i7.

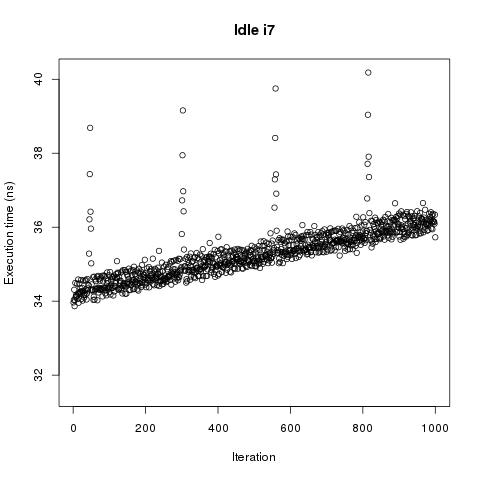
No surprise time dependence didn’t disappear but we got peaks at regular intervals. Probably those are GC related. They were completely masked by random jitter in previous measurement. We can force GC before every benchmark with -g switch.

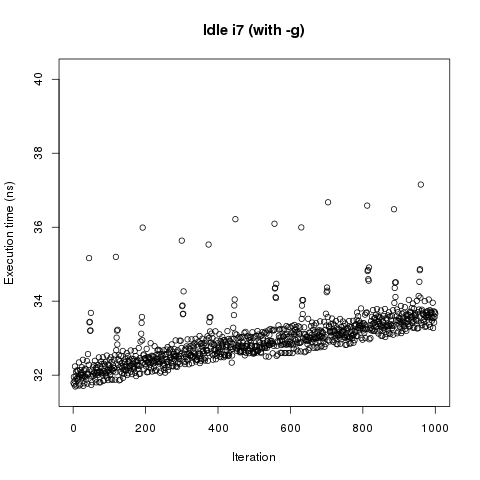
It didn’t help. Spikes didn’t go away only become more frequent. So there’s some strange effect which increases benchmark run time with every iteration. Cause of such weird behavior should be found.

P.S. Now if we return to the first plot we can see that distribution of run times do have tail at big t so we should expect that proper confidence interval would be quite asymmetric. This tail also limits attainable precision.

haskell-mode is amazing piece of software but unfortunately it lacks documentation which describe available features. Without it only way to discover such features is to look into source code. This is time consuming process although rewarding. I describe here things I found in the current git. Some of functions are not imported by default so module where they defined should be imported manually.

Navigate imports

Jumping to import list to add/remove/tweak something is very frequent activity. Finding import is not that difficult they are always in the beginning of the file. Real problem is find place on which you worked before. Functions haskell-navigate-imports and haskell-navigate-imports-return fix that problem. First cycle though import list and second return you to place where you were before.

They are not binded to any key so one have to add them using hook. here is my choice of bindings:

(require 'haskell-navigate-imports)
(add-hook-list 'haskell-mode-hook (lambda () (
  (local-set-key (kbd "M-[") 'haskell-navigate-imports)
  (local-set-key (kbd "M-]") 'haskell-navigate-imports-return)))

Inserting/removing SCC

Another very useful feature is quick adding/removing SCC (Set Cost Centre) annotations which are often necessary to get accurate profiling information. While -auto-all option annotate every top level declaration it’s not always enough.

Just as their names suggest function haskell-mode-insert-scc-at-point and haskell-mode-kill-scc-at-point insert and remove SCC pragmas without tiresome typing. Of course they work best when binded to some key chain.

Indenting/unindenting code blocks at once.

Last item in the list is function for changing indentation of complete code blocks. Here is example of indenting where block by two spaces:

foo = ...              foo = ...
  where           | →  __    where
   a = 1          | →  __      a = 1
   b = a + 1      | →  __      b = a + 1

This functionality provided by haskell-move-nested. This function is not binded to anything too nor could used interactively with M-x. Here are bindings suggested by documentation:

(reqire 'haskell-move-nested)
(add-hook-list 'haskell-mode-hook (lambda ()
  (define-key haskell-mode-map (kbd "M-<left>")
    (lambda ()
      (interactive)
      (haskell-move-nested -1)))
  (define-key haskell-mode-map (kbd "M-<right>")
    (lambda ()
      (interactive)
      (haskell-move-nested  1)))))

In previous post on generic estimators: “Generalizing estimators” four type classes were introduced:

class Sample a where
  type Elem a :: *
  foldSample  :: (acc -> Elem a -> acc) -> acc -> a -> acc

class NullEstimator m where
  nullEstimator :: m

class FoldEstimator m a where
  addElement  :: m -> a -> m

class SemigoupEst m where
  joinSample :: m -> m -> m

Sample exists only because Foldable couldn’t be used and have only methods which are strictly necessary. Foldable require that container should be able to hold any type. But that’s not the case for unboxed vector and monomorphic containers like ByteString could not be used at all.

Laws for other type classes are quite intuitive and could be summarized as: evaluating statistics for same sample should yield same result regardless of evaluation method. However because in many cases calculations involve floating point values result will be only approximately same.

First joinSample is obviously associative because merging of subsamples is associative. Moreover it most cases it’s commutative because order of elements doesn’t matter by definition of statistics. Probably there are cases when calculation could be expressed with this API and order will matter but I’m not aware about them.

(a `joinSample` b) `joinSample` c = a `joinSample` (b `joinSample` c)
a `joinSample` b = b `joinSample` a

These are laws for commutative semigroup. So estimators form semigroup. If we add zero element we’ll get a monoid. In this context zero element is empty sample and nullEstimator corresponds to empty sample:

x `joinSample` nullEstimator = x
nullEstimator `joinSample` x = x

Thus we got a monoid. Unfortunately Monoid type class from base couldn’t be used since it require both zero element and associative operation to be defined. It’s however entirely possible to have estimator where statistics for empty sample is undefined or estimator without joinSample.

Last law says that calculating statistics using joinSample or with fold should yield same result.

fold addElement (fold addElement m xs) ys =
  fold addElement nullEstimator ys `joinSample` fold addElement m xs