Criterion is excellent benchmarking framework. It easily could be the best one. It’s easy to use, able to generate nice reports. It attempts to get estimate of benchmark run time and error of this estimate. Strangely I never saw attempts to validate these measurements. Criterion is widely used but many questions important questions are still open:

1. Are measurements biased? OS scheduler and GC pauses tend to increase benchmark running time make distribution of run times asymmetric with tail at large t. This could easily lead to biased results.

2. Are error estimates reliable? Criterion could under- or overestimate errors. They are overlooked most of the time but still worth checking.

3. How precise are measurements. It’s easy to see 200% difference and be sure that it exists. But what about 20%? Or even 5%? What is measurable difference?

4. And of course there’s something else. There’s always something unexpected.

Correctness of error estimates

In this post I’ll try to check whether error estimates are reliable. This is very simple test. Measure same quantity many times and check what part of measurement fall into confidence interval. If too small fraction of event falls in error are underestimated and overestimated otherwise. All measurements were done with GHC 7.6.1 and criterion-0.6.2.1.

Here is program I used. It benchmarks exp function 1000 times. exp is cheap so here we probing regime of cheap functions which take many iterations to measure.

import Criterion.Main

main :: IO ()
main = defaultMain $ replicate 1000 $ bench "exp" $ nf exp (1 :: Double)

Benchmark was run on 6-core AMD Phenom-II with active X session. First thing to plot it run time vs number of benchmark. Here it is:

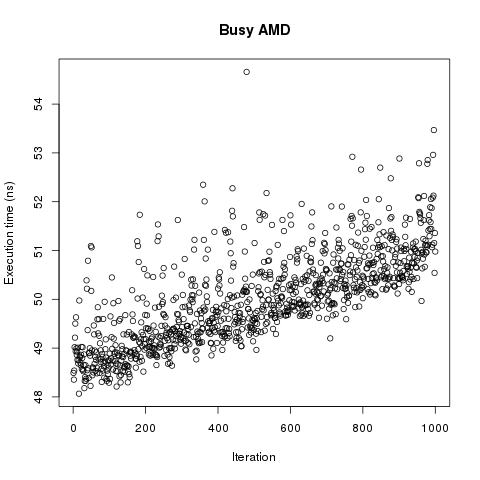
Now we have problem. Run time linearly depends on the number of benchmark or on the time. This test doesn’t discriminate between them. There is little doubt in existence of the effect but let repeat measurements in cleaner conditions. Second run was performed on completely idle core i7.

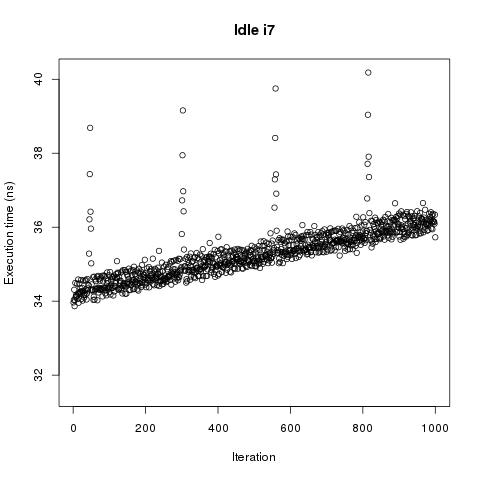
No surprise time dependence didn’t disappear but we got peaks at regular intervals. Probably those are GC related. They were completely masked by random jitter in previous measurement. We can force GC before every benchmark with -g switch.

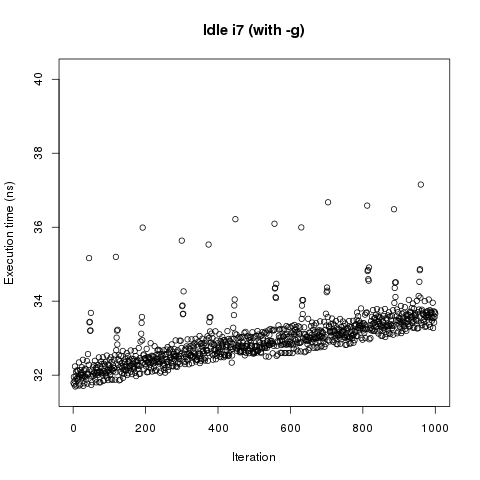
It didn’t help. Spikes didn’t go away only become more frequent. So there’s some strange effect which increases benchmark run time with every iteration. Cause of such weird behavior should be found.

P.S. Now if we return to the first plot we can see that distribution of run times do have tail at big t so we should expect that proper confidence interval would be quite asymmetric. This tail also limits attainable precision.

Links

• Home page
• All posts
• RSS feed

Tags